Josephson Vortex Qubit
My research on condense matter physics focuses on the study of classical and quantum dynamics of magnetic vortices in long Josephson junctions (LJJ). An LJJ is a tri-layer micro device in which a very thin insulator layer is sandwiched between two relatively thick superconductor layers. This structure supports the non-linear dynamics of magnetic vortices along the insulating layer and provides the host of potential of designing superconducting devices such as Superconducting Quantum Interference Devices (SQUIDs), high frequency generator and quantum computers to name some. I am currently studying the possibility of designing quantum bits (qubits) by making use of quantum dynamics of Josephson vortexes.
A qubit, which is a quantum counterpart of a classical bit, is the fundamental unit necessary for making quantum computers. A quantum computer benefits from the superposition principle of quantum mechanics because it can take many inputs as the superposed single input. This property makes quantum computers inherently parallel and can behave as a supercomputer made from several parallel processors. When used with the quantum algorithms tailored for such computers, they open the possibility of a new window which can bring revolution in some aspects of computing such as effective simulation of quantum systems, factoring of large prime numbers, and searching in large databases.
Tremendous progress has recently been made in the theoretical and experimental investigations of designing different kinds of qubits. But design of a fully working quantum computer still poses great challenges to us. One of the main challenges is obtaining a long enough decoherence time so that two qubits can communicate without losing information.
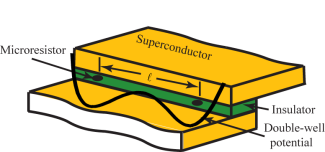
Currently, I am exploring the possibilities of realizing Josephson vortex quantum bits (JVQ) from LJJs. When two impurities (also known as microresistors) are implanted at suitable distance in the insulating layer of the LJJ, they trap magnetic vortices (also known as Josephson vortices or fluxons) by creating a double well potential as shown in the figure below.
When a fluxon trapped in a well (figure below, left) tunnels quantum mechanically to another well, a two-state system is created (figure below, right). This two-state system may work as a qubit.
Our work shows that relatively long decoherence time can be obtained from a JVQ. I have also estimated the Concurrence between two JVQs coupled via magnetic induction effect between two LJJs. The study shows nearly perfect values can be achieved by adjusting the junction parameters. Concurrence is a way of measuring the entanglement between the qubits. Entanglement between the qubits is necessary to realize quantum gates and hence the quantum computers.
I use the perturbed sine-Gordon equation, a non-linear partial differential equation, to model the dynamics of fluxons in the LJJ with impurities. By describing the motion of the fluxons in a center coordinate of a single fluxon, I come up with the double-well potential potential shown in the figure above. The quantum tunneling of a fluxon from one well to the other is used as the probability of a spin flip of the two state system. The evolution of the spin system in the presence of bath is described by using the spin-boson model from which I estimate the decoherence time of the qubits. The tunneling is also used to find the extent of interaction between the fluxons in two different qubits, which gives the measure of the entanglement.